💡𝚂𝗆𝖺𝗋𝗍𝗆𝖺𝗇 𝙰𝗉𝗉𝗌📱
- 4 Posts
- 237 Comments

 11·4 months ago
11·4 months agoAccording to me, talking about the origin of the 0.999…
Right. So not according to the meme, which doesn’t tell us where the 0.999… comes from. Nor the 1 - could be an integer, floating point, or an estimation. Thanks for playing.
And if you don’t then you can no longer claim they are still equal.

 11·4 months ago
11·4 months agoyou can substitute anywhere
And if you are rearranging algebra you have to do the exact same thing on both sides, always
This isn’t about limits of accuracy
According to who? Where does it say what it’s about? It doesn’t.
please show me how basic arithmetic can make 0.999
You still haven’t shown why you’re limiting yourself to basic arithmetic. There isn’t anything at all in the meme to indicate it’s about basic arithmetic only. It’s just some Maths statements with no context given.
then a correct use of the system must be applicable to everything, right?
Different systems for different applications. Sometimes multiple systems for one problem (e.g. proofs).
You shouldn’t need a new system like algebra to be correct, right?
Limits of accuracy isn’t algebra.

 11·4 months ago
11·4 months agonot taught yet
What do you mean not taught yet? There’s nothing in the meme to indicate this is a primary school problem. In fact it explicitly has a picture of an adult, so high school Maths is absolutely on the table.
There is no method by which basic arithmetic and decimal notation can turn 0.999… into 1.
In high school we teach that they are the same thing. i.e. limits of accuracy, 1 isn’t the same thing as 1.000…, but rather 1+/- some limit of accuracy (usually 1/2). Of course in programming it matters if you’re talking about an integer 1 or a floating point 1.
If someone uses these systems as they were taught, they will get told they’re wrong for doing so
The only people I’ve seen get things wrong is people not using the systems correctly (such as the alleged “proof” in this thread, which broke several rules of Maths and as such didn’t prove anything), and it’s a teacher’s job to point out how to use them correctly.

 11·4 months ago
11·4 months agoP.S.
“We do it like that, therefore, it is right”
Yep, Maths teachers do it right. :-)

 11·4 months ago
11·4 months agoYou’re just another yank
BWAHAHAHA! I see you still didn’t learn to check facts first. 😂😂😂

 11·4 months ago
11·4 months agoX times 10 is 10x
10x is 9.9999999…
As I said, they didn’t substitute on both sides, only one, thus breaking the rules around rearranging algebra. Anything you do to one side you have to do to the other.

 11·4 months ago
11·4 months agoP.S. you proved my point
The only people who think there’s something wrong with PEMDAS are people who have forgotten one or more rules of Maths.
https://www.youtube.com/watch?v=lLCDca6dYpA
…oh wait I remember that
Well, you seem to have forgotten that the woman in that video isn’t a Maths teacher, which would explain why she’s forgotten the rules of The Distributive Law and Terms.
until you gave up
I didn’t give up, you did.
I suggest we don’t do it again but instead, you review the thread
I suggest you check some Maths textbooks, instead of listening to a Physics major.

 11·4 months ago
11·4 months agothose systems are giving an incorrect answer
When there’s an incorrect answer it’s because the user has made a mistake.
Instead of telling those people they’re wrong
They were wrong, and I told them where they went wrong (did something to one side of the equation and not the other).

 11·4 months ago
11·4 months agoMaths teachers are constantly wrong about everything
Very rarely wrong actually.
the abomination that is PEMDAS
The only people who think there’s something wrong with PEMDAS are people who have forgotten one or more rules of Maths.

 11·4 months ago
11·4 months agoyou can prove it with math
Not a proof, just wrong. In the “(substitute 0.9999… = x)” step, it was only done to one side, not both (the left side would’ve become 9.99999), therefore wrong.

 11·5 months ago
11·5 months agoThe rules and the acronyms describe different things.
No, they don’t.
If you have to make more rules to say M and D are the same,
I didn’t make more rules - that’s the existing rules. Here’s one of many graphics on the topic which are easy to find on the internet…
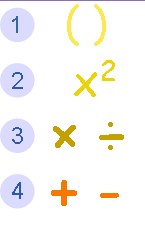
…that’s one of the two examples you used?
Yes. Did you try looking for one and ramping it up to the most difficult level? I’m guessing not.
IT IS AMBIGUOUS IN THIS POST
No, it isn’t. Division before subtraction, always.
ALL EXAMPLES I HAVE SHOWN
None of those have been ambiguous either, as I have pointed out.
That is the problem at hand.
The problem is people not obeying the rules of Maths.
There is no real problem solving in trying to decipher poorly written shit
It’s not poorly written. It’s written the exact way you’d find it in any Maths textbook.

 11·5 months ago
11·5 months agoYou are adding more rules
I’m stating the existing rules.
If all that matters is higher orders first
I don’t even know what you mean by that. We have the acronyms as a reminder of the rules, as I already said.
I know operators apply to the numbers to their right.
If you know that then how did you get 2-2+2=-2?
With 2/22, you don’t know if it is 22/2, or 2/(2*2)
Yes you do - left associativity. i.e. there’s no brackets.
When you are dividing by numbers, you put them all in the denominator
Only the first term following a division goes in the denominator - left associativity.
BY CONVENTION, as I said. You don’t have to repeat what I said a second time.
I didn’t. You said it was a convention, and I corrected you that it’s a rule.
It’s not like you could have tried in your head different orders to combine 3 numbers.
addition first
2-2+2=4-2=2
subtraction first
2-2+2=-2+2+2=-2+4=2
left to right
2-2+2=0+2=2
3 different orders, all the same answer

 1·5 months ago
1·5 months agoWho’s on first? :-)

 21·5 months ago
21·5 months agoMultiplication comes before division in some forms, like PEMDAS. In the example I use, this changes the answer
If you have both multiplication and division then you do them left to right. PEMDAS doesn’t mean multiplication first, nor does BEDMAS mean division first. It’s PE(MD)(AS) and BE(DM)(AS) where the bracketed parts are done left to right.
you should specify what it is operating on
Left associativity means it always operates on the following term. i.e. terms are associated with the sign on their left.
The minus sign only applies to the middle term, by convention
By the rule of left associativity.
But if you use one of these acronyms, you end with this expression evaluating to -2
No it doesn’t. How on Earth did you manage to get -2?
all these acronyms end up being useless waste of time
No they’re not, but I don’t know yet where you’re going wrong with them without seeing your working out.

 22·5 months ago
22·5 months agoEven your “BODMAS” isn’t universal, lots of people learn “PEMDAS” or “BEDMAS”
The rules are universal, only the mnemonics used to remember the rules are different
except for facebook and twitter
… and high school Maths textbooks, and order of operations worksheet generators, and…
2/2*2 It is 0.5 or 2 depending on order.
It’s always 2. #MathsIsNeverAmbiguous

 21·5 months ago
21·5 months agoNo, it isn’t. Division before subtraction.





No, you haven’t shown that, because you haven’t shown yet that 9x=9. Welcome to why this doesn’t prove anything. You’re presuming your result, then using it to “prove” your result.
What we know is that the right hand side is 10 times 0.9999…, so if you want to substitute x=0.99999… into the right hand side, then the right hand side becomes 10x (or 9x+x)… which only shows what we already know - 10x=10x. Welcome to the circularity of what you’re trying to achieve. You can’t use something you haven’t yet proven, to prove something you haven’t yet proven.